Hypothesenprüfende Untersuchungen: der t-Test

Einleitung

Hypothesenprüfende Untersuchungen werden in der Sozialforschung eingesetzt, um Annahmen über Zusammenhänge, Unterschiede und Veränderungen vorher ausgewählter Merkmale innerhalb einer Population zu testen. In diesem kleinen Aufsatz über die Grundlagen des t-Tests wird ein Bogen geschlagen von der Hypothesenformulierung bis hin zur konkreten Durchführung eines Tests.

Was ist eine Hypothese?

Bevor Annahmen über eine Population getestet werden können, müssen aus Voruntersuchungen, eigenen Beobachtungen und theoriegeleiteten Recherchen Vermutungen über die Ausprägung eines Merkmals bzw. allgemein: über den Forschungsgegenstand formuliert werden. Dabei wird eine Formulierung gewählt, die allgemein formuliert ist und sich in den Einschränkungen nicht an der Stichprobe orientiert. Nach allgemeinem Forschungsparadigma (nach Popper) müssen wissenschaftliche Hypothesen zumindest potenziell widerlegbar sein, es dürfen also keine metaphysischen oder spekulative Aussagen über den Forschungsgegenstand getroffen werden. Idealerweise reflektiert die Hypothese den Wissensstand in dem zu untersuchenden Problemfeld. Je nach Forschungsinteresse können Hypothesen nach unterschiedliche Zielrichtungen formuliert werden. Interessiert ein Zusammenhang zwischen zwei oder mehr Merkmalen, wird eine sog. Zusammenhangshypothese formuliert (Zwischen „Krankmeldungen“ und „Stress am Arbeitsplatz“ besteht ein positiver Zusammenhang). Unterschiede in der Ausprägung werden in einer Unterschiedshypothese formuliert (Männer und Frauen unterscheiden sich in Bezug auf ihre Bildungsrendite). Werden Änderungen der Eigenschaften über die Zeit betrachtet, sind Veränderungshypothesen zu formulieren (Werden Aufgaben wiederholt, liegen Lerninhalte in hoher Elaboration vor).

Für eine Untersuchung eines Forschungsgegenstandes wird also eine in einem Konditionalsatz klar und allgemein formulierte, potenziell widerlegbare Annahme formuliert. Erst dann kann eine Hypothese sinnvoll getestet werden.

Planung einer Untersuchung

Um aber eine Hypothese zu testen wird eine Operationalisierung (Bridgeman, 1927) des Merkmals unabdingbar. Eine operationale Definition standardisiert einen Begriff durch Angabe der Operationen, die zur Erfassung des durch den Begriff bezeichneten Sachverhalts notwendig sind, oder durch Angabe von messbaren Ereignissen, die das Vorliegen des Sachverhalts anzeigen [Bortz & Döring, 2002].

Eine genaue Planung des Ablaufs der Untersuchung unterstützt die Testgütekriterien Reliabilität, Objektivität und Validität.

Ist die Hypothese formuliert, sind die Operationalisierungen definiert und der Ablauf geplant, kann die Untersuchung starten.

Eine der üblichen statistischen Tests für hypothesenprüfende Untersuchungen ist der sogenannte t-Test.

Der t-Test

Um eine Unterschiedshypothese zu testen, formuliert man idealerweise eine Unterschiedshypothesenpaar z.B. H₀: „Es gibt einen Unterschied in der Lerngeschwindigkeit zwischen Männern und Frauen“ H₁: „Es gibt keinen Unterschied in den Lerngeschwindigkeiten zwischen Männern und Frauen“. Für dieses Hypothesenpaar wird ein t-Test empfohlen. Dieser Test vergleicht Mittelwerte je einer Stichprobe aus Männern beziehungsweise Frauen 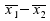. Dabei wird implizit angenommen, dass die Varianz des getesteten Merkmals in beiden Stichproben gleich ist. Erreicht wird das über die Z-Standardisierung der Verteilungskurve der Stichproben. Nach Z-Standardisierung erhält man eine transformierte, normalverteilte Kurve mit Mittelwert μ = 0 und der Streuung σ = 1. 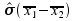Der statistische Testwert t folgt für n>30 (n: Anzahl der Probanden) der t-Verteilung, wenn die geschätzten Populationsvarianzen homogen sind.

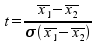
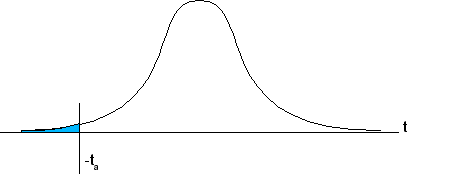
Gerichtete Alternativhypothesen H₁ („ist größer...“, „ist kleiner...“) werden mit einem einseitigen Test,

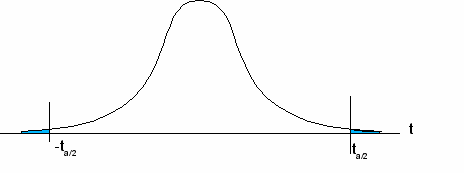
ungerichtete Alternativhypothesen H₁ („es gibt einen Unterschied...“) werden mit einem zweiseitigen Signifikanztest geprüft.

Das Signifikanzniveau wird willkürlich festgelegt. Den Konventionen folgend wird ein Signifikanzniveau von a = 0,05 bzw. für hoch signifikante Untersuchungen a = 0,01 empfohlen.

Liegt der experimentell bestimmte Wert für t außerhalb der Grenzen die durch das Signifikanzniveau vorgegeben sind (in der Grafik farbig markiert), muss die H0 zugunsten der Alternativhypothese H1 abgelehnt werden. Liegt der experimentell bestimmte Wert für t innerhalb des Bereichs, kann aber ohne weitere Untersuchungen nicht angenommen werden, dass die H0 gilt. 

Bei Entscheidungen auf Grund empirischer Tests anhand einer Stichprobe können zwei Arten von Fehlern auftreten:

Der α – Fehler ist durch das Signifikanzniveau bereits bestimmt. Die Wahrscheinlichkeit liegt bei a = 0.05 bzw. a = 0,01. Die Wahrscheinlichkeit einen β – Fehler zu begehen ist unbestimmt. Bortz & Döring (2002) plädieren für die Einführung einer gleich großen α- und β – Fehler Wahrscheinlichkeit bei gleich gravierenden Folgen eines α – Fehlers und eines β – Fehlers. Cohen (1988) geht von einem – auf die Domäne der sozialwissenschaftlichen Forschung beschränkten – Verhältnis von α- / β – Fehler von 1 zu 4 aus. Daraus ergibt sich für das Signifikanzniveau von a = 0,05 eine β – Fehler-Wahrscheinlichkeit von b = 0,20.

Zusammenfassung.

Der t-Test eignet sich zur Hypothesenprüfung von Unterschiedshypothesen in denen ein Merkmal wissenschaftlich und messbar operationalisiert werden kann. Der t-Test untersucht eine Mittelwertsdifferenz zweier Stichproben. Dabei ist es unerheblich, ob die Stichproben abhängig (d.h. zwei mal getestet werden) oder unabhängig sind. Liegt der gemessene t-Wert unterhalb des Signifikanzniveaus, muss die H₀ zugunsten der Alternativhypothese H₁ abgelehnt werden. Liegt der gemessene t-Wert innerhalb des Konfidenzintervalls, kann die H₀ nicht ohne weiteres angenommen werden, denn die Entscheidung ist durch die Wahrscheinlichkeit einen β – Fehler zu begehen belastet.